

La forza elettromotrice di un generatore elettrico di qualsiasi tipo
[batteria di pile, di accumulatori, cella a combustibile (fuel cell), batteria
fotovoltaica, dinamo, alternatore] corrisponde al lavoro, per unità di carica
elettrica, che all'interno del generatore viene compiuto dalle forze non
conservative per determinare al polo positivo una carenza di elettroni ed al
polo negativo un eccesso di elettroni, sia quando il generatore è a vuoto,sia
quando eroga potenza elettrica.
Fatta questa premessa, si può dire che, nel
caso di un generatore di tensione continua,la f.e.m. è il lavoro che il campo
elettromotore (non il campo elettrico) compie per spostare, all'interno del
generatore, la carica unitaria positiva dal polo negativo al polo positivo
(definizione elettrotecnica), oppure (definizione elettronica) il lavoro che il
campo elettromotore compie per spostare, all'interno del generatore, la carica
unitaria negativa dal polo positivo al polo negativo.
Per spiegare meglio il
concetto possiamo pensare al lavoro che,stando in piedi, dovremmo compiere con
la forza muscolare (analoga al campo elettromotore) delle braccia per sollevare
un peso P al di sopra della testa e mantenerlo stabilmente in tale
posizione. E' chiaro che dovremmo fornire al peso P, attraverso il lavoro
muscolare, un'energia potenziale gravitazionale pari al prodotto PH =
MgH,essendo H l'altezza alla quale il peso viene sollevato,
g =
9,81 m/s2 l'accelerazione di gravità ed M la massa.
La
d.d.p. gravitazionale gH (lavoro gravitazionale per unità di massa) tra
il suolo e l'altezza H , si ottiene dividendo il lavoro gravitazionale
L = PH = M gH per la massa M, e corrisponde alla d.d.p.
elettrico.
[ d.d.p. elettrico = Le/Q (lavoro elettrico per unità di
carica)].
In questo esempio la grandezza analoga alla f.e.m. è il rapporto
tra il lavoro muscolare compiuto Lm e la massa M del corpo che è
stato sollevato all'altezza H, ed è uguale alla d.d.p. gravitazionale
gH.
Analogamente, all'interno di un generatore elettrico il rapporto
tra la forza non conservativa, che sposta gli elettroni dal polo positivo e li
accumula a quello negativo, e la carica elettrica totale spostata, è appunto il
cosiddetto campo elettromotore, da non confondere con il campo elettrostatico,
che è invece conservativo, in quanto il lavoro da esso fatto in un ciclo (dal
punto A al punto B con ritorno in A) è sempre nullo, indipendentemente dal
percorso che si considera.
In una batteria di pile o di accumulatori, oppure
in una cella a combustibile, il campo elettromotore (di natura non elettrica) è
dovuto all'energia chimica delle reazioni coinvolte.
In una batteria
fotovoltaica il campo elettromotore è dovuto all'energia elettromagnetica dei
fotoni della radiazione solare, che generano in un semiconduttore le coppie
elettrone-buca che si allontanano verso i poli generando la f.e.m..
In una
dinamo o in un alternatore il campo elettromotore è dovuto alla forza di Lorentz
F = evB, che agisce sugli elettroni di un filo conduttore che si
sposti con velocità v in un campo magnetico di induzione B,
perpendicolare alla velocità v .
Nel caso dell'avvolgimento secondario
di un trasformatore, la f.e.m. indotta secondaria è dovuta al campo elettrico
indotto, non conservativo, che si genera per induzione elettromagnetica (Legge
di Faraday-Neumann-Lenz).
In tutti questi casi, anche quando il circuito è
aperto, il campo elettromotore compie un lavoro iniziale necessario ad
accumulare gli elettroni al polo negativo (o al polo temporaneamente negativo
durante un semiperiodo di una tensione alternata) ed a generare la tensione
elettrica (d.d.p.) V che uguaglia, istante per istante, il lavoro fatto
dal campo elettromotore per unità di carica, e che corrisponde alla f.e.m.
:
( V = Lavoro del campo elettromotore /Q = f.e.m.) .
Quando invece
il generatore eroga potenza , il passaggio di corrente determina il ritorno
degli elettroni al polo positivo, attraverso il circuito esterno (carico) , ed
un conseguente ulteriore lavoro del campo elettromotore all'interno del
generatore per riportarli al polo negativo , e così via, finchè il circuito è
chiuso.
1) Per spiegare la connessione tra campo elettromotore e campo elettrico mi
avvalgo del classico esempio della pila (pila primaria) . Il funzionamento di
una pila non dipende dalla d.d.p. di contatto tra due metalli diversi , per
esempio rame e zinco, ma dal campo elettromotore che nasce dal contatto tra un
metallo ed una soluzione elettrolitica:
Consideriamo un elettrodo di zinco
immerso in una soluzione di un suo sale (per es. ZnSO4) oppure in una
soluzione acida. Se la soluzione è molto povera di ioni del metallo, si verifica
un passaggio di ioni, per diffusione,quindi per un fenomeno termodinamico
dipendente dalla temperatura assoluta T, dal metallo alla soluzione, per effetto
di forze che dipendono dalle proprietà della struttura cristallina del metallo .
In questo caso il metallo tende a sciogliersi nella soluzione per effetto di una
tensione di soluzione P che supera la pressione osmotica p degli ioni in
soluzione, caricandosi negativamente a causa degli ioni positivi rilasciati in
soluzione ed assumendo una d.d.p.Vp (potenziale di elettrodo), data dalla
formula della teoria della pila di Nernst:
Vp = (RT/nF) ln (P/p), dove R è la
costante universale dei gas, n è la valenza degli ioni, T è la temperatura
assoluta (°K) della soluzione , F = 96500 coulomb è la costante di Faraday che
interviene in tutti i fenomeni elettrolitici ed ln(P/p) è il logaritmo naturale
del rapporto tra P e p. Il passaggio di ioni dal metallo alla soluzione continua
fino a quando la d.d.p. elettrico tra metallo e soluzione non diventa tale da
generare un campo elettrico capace di equilibrare il campo elettromotore
connesso alla tensione di soluzione P del metallo. Raggiunto l'equilibrio, il
numero di ioni metallici che passano, in media, nell'unità di tempo, dal metallo
alla soluzione è uguale a quello degli ioni metallici che dalla soluzione si
depositano sul metallo. L'equilibrio viene meno se con un conduttore viene
chiuso il circuito tra il metallo e la soluzione, in quanto la differenza tra il
campo elettromotore F ed il campo elettrico E determina un
passaggio di corrente attraverso la soluzione elettrolitica , avente una
conducibilità elettrica Cs direttamente proporzionale alla concentrazione
ionica. Pertanto dalla legge di Ohm si ottiene la densità di corrente elettrica
J nella soluzione (il modulo del vettore J rappresenta l'intensità
di corrente per unità di superficie) :
J= Cs (F - E).
Quando invece il generatore è a vuoto, la densità di corrente J è
nulla e pertanto il campo elettromotore F è uguale e contrario al campo
elettrico E da cui dipende la tensione (a vuoto) tra metallo e
soluzione.
Se invece si considerano due elettrodi diversi, per esempio rame e
zinco oppure carbone di storta (carbone metallico) e zinco, immersi in una
soluzione acida, si ottiene una d.d.p. a vuoto (f.e.m. della pila) , data dalla
somma algebrica tra la semipila zinco/soluzione e quella rame/soluzione
(carbone/soluzione) . Infatti, mentre lo zinco si scioglie nell'acido,
caricandosi negativamente (in quanto la tensione di soluzione P supera la
pressione osmotica p),il rame o il carbone , sui quali si depositano ioni
metallici, si caricano positivamente (in quanto la tensione di soluzione P è
inferiore alla pressione osmotica p).
Il passaggio di corrente cesserà quando
lo zinco sciogliendosi nell'acido incrementerà gradualmente la pressione
osmotica fino a farle raggiungere il valore della tensione di soluzione P del
metallo [ln (P/p) = ln 1 = 0].
Se consideriamo il circuito formato da una
batteria di pile o di accumulatori e da un utilizzatore collegato ai suoi poli
(lampadina, motorino a corrente continua, ecc. …) , per effetto del passaggio
della corrente elettrica causata dal campo elettromotore (di origine
elettrochimica), all'interno della batteria, e precisamente nella soluzione
elettrolitica, si stabilisce un campo elettrico
Es = J/Cs = (I/S)/Cs,
essendo I l'intensità di corrente, S l'area degli elettrodi e Cs la
conducibilità della soluzione elettrolitica.
Il prodotto del campo Es per la
distanza d tra gli elettrodi fornisce la caduta di tensione Vi = Es d interna
alla batteria . Pertanto la d.d.p. Vc ai poli della batteria, sotto carico, è
data dalla differenza tra la f.e.m. Eb (tensione misurata tra i poli, a vuoto) e
Vi:
Vc = Eb -Vi = Eb - Ri I, essendo Ri I = Es d la caduta di tensione
interna dovuta alla resistenza interna Ri della batteria.
2) Il campo
elettrostatico generato nello spazio dalle cariche elettriche ferme in
determinate posizioni, e così anche quello dovuto al passaggio della corrente
continua all'interno di un conduttore ( V = RI), sono entrambi campi elettrici
conservativi. Un campo si dice conservativo, se il lavoro da esso compiuto in
uno spostamento tra due punti A e B dipende soltanto dalle coordinate dei due
punti e non dal percorso (traiettoria).
In questo caso il lavoro compiuto
dal campo si può esprimere come differenza tra i valori assunti nei due punti da
una funzione U delle coordinate, che prende il nome di energia potenziale. Un
noto esempio è quello del campo di gravità, quasi costante, in prima
approssimazione, in prossimità della superficie terrestre. Infatti il lavoro L =
mg (HA - HB) che la forza peso compie su un corpo di massa
m che si sposta dal punto A al punto B, non dipende dal percorso tra A e B,
poiché la forza di gravità è sempre diretta lungo la verticale, ma soltanto
dalla differenza di quota H tra A e B. In modo equivalente si può dire che un
campo è conservativo se è nullo il lavoro compiuto in un percorso ciclico (da A
a B ad A). Il fatto che il campo elettrostatico sia conservativo permette di
calcolare il lavoro e quindi l'energia che un corpo carico acquista o cede
quando si sposta nel campo elettrico, attraverso la differenza di potenziale
elettrostatico (energia potenziale elettrostatica per unità di carica elettrica)
VA-VB:
L = q[VA-VB]. Questa
proprietà del campo elettrico stazionario è molto importante, in quanto consente
di semplificare la trattazione di una vasta categoria di problemi in termini di
tensioni (d.d.p. misurabili con voltmetri), senza essere costretti a ricorrere a
misure di campo (forza elettrica per unità di carica).
Sono invece non
conservativi tutti i campi elettrici variabili nel tempo,come quelli generati
nei fenomeni di induzione elettromagnetica (legge di Faraday-Neumann-Lenz) e di
propagazione delle onde elettromagnetiche, nei quali la non stazionarietà del
campo elettrico implica la connessione tra campo elettrico e campo magnetico
variabile nel tempo, descritta dalla seconda equazione di Maxwell.
1) L'operatore differenziale divergenza di un vettore V, espresso con
la notazione
div V = DxVx +
DyVy + DzVz , è una funzione scalare
delle coordinate x,y,z , data dalla somma delle derivate parziali
Dx,Dy, Dz delle componenti cartesiane del
vettore.
Il suo significato fisico è connesso alle sorgenti del campo
vettoriale V (campo gravitazionale, campo elettrico, campo magnetico,
campo di velocità di un fluido) .
Esempio: la divergenza dei campi
gravitazionale ed elettrico è una funzione scalare diversa da zero soltanto nei
punti dello spazio nei quali sono localizzate, rispettivamente, le masse o le
cariche elettriche che rappresentano le sorgenti del campo; essa è invece nulla
in tutti i punti dello spazio nei quali non esistono masse né cariche
elettriche, ed in tali punti il campo (gravitazionale o elettrico) si definisce
a divergenza nulla o solenoidale, dal greco sole'n, tubo. Infatti, in tal
caso, le linee di forza del campo (newtoniano o coulombiano) passanti per i
punti di due linee chiuse non giacenti sullo stesso piano, individuano un "tubo
di forza", che ricorda l'andamento delle linee di flusso di un fluido (liquido o
gas) all'interno di un tubo nel quale non esistano né sorgenti né pozzi per il
fluido.
Pertanto la divergenza del campo gravitazionale generato da tutti i
corpi del sistema solare è diversa da zero soltanto nelle regioni spaziali
interne al sole, ai pianeti, ai satelliti ed agli asteroidi,che sono le sorgenti
del campo, nulla all'esterno di essi.

Ciò significa, ricordando la ben nota rappresentazione di Faraday in uso per
i campi vettoriali, che, considerata una qualsiasi superficie chiusa contenente
corpi celesti, oppure cariche elettriche positive e negative la cui somma
algebrica sia diversa da zero, il flusso del campo , rispettivamente
gravitazionale o elettrico, uscente dalla superficie chiusa è diverso da zero
(Teorema di Gauss).
Se invece si considera una superficie chiusa di forma
qualsiasi, non contenente sorgenti del campo ( corpi celesti o cariche
elettriche), il numero delle linee di forza entranti attraverso la superficie è
sempre uguale a quello delle linee di forza uscenti da essa (campo solenoidale).
Se invece si considera il campo magnetico, e si tiene presente la ben nota
esperienza della calamita spezzata, che dimostra che in natura non esistono poli
magnetici isolati, si deduce subito che, eseendo sempre chiuse le linee di forza
magnetiche, il campo magnetico è sempre solenoidale (a divergenza nulla), in
tutti i punti dello spazio

2) L'operatore gradiente di un campo scalare è legato alla variazione
spaziale della grandezza fisica che si considera (temperatura, concentrazione di
una sostanza, pressione atmosferica, densità di carica o di materia). Il termine
deriva dal latino gradus, passo, in quanto, in ogni punto di coordinate
x,y,z la direzione ed il verso secondo cui una grandezza scalare (t,p,c, ecc… )
varia maggiormente coincidono con la direzione ed il verso del gradiente, che è
un vettore perpendicolare, in tre dimensioni, alle superfici di livello
(superfici costituite da tutti i punti dello spazio nei quali la grandezza
scalare assume lo stesso valore), ed in due dimensioni, alle curve di livello
(curve passanti per tutti i punti del piano nei quali la grandezza scalare
assume lo stesso valore :
Esempio:
gradiente barico, relativo alla
variazione della pressione atmosferica p in funzione delle coordinate
geografiche (latitudine, longitudine, altezza sul livello del mare)
grad p =
nabla p = Dxp i+ Dyp j + Dzp
k, dove l'operatore nabla, che si indica con una delta maiuscola
capovolta, rappresenta un vettore infinitesimo avente per componenti gli
operatori di derivazione parziale rispetto alle variabili x,y,z, e
i,j e k sono i versori (vettori di modulo unitario) degli
assi cartesiani del sistema di riferimento.
Il gradiente barico è sempre
perpendicolare alle curve isobare , curve di livello passanti per i punti
corrispondenti allo stesso valore della pressione atmosferica, ed è diretto
verso le isobare relative a pressioni crescenti.
I venti sono causati dal
gradiente barico e sono diretti verso i punti nei quali la pressione è minore,
in senso opposto al gradiente. Bisogna tuttavia tenere presente che,
nell'emisfero boreale, il moto delle masse d'aria lungo le isobare,
rispettivamente antiorario per le aree cicloniche, cioè quelle con area centrale
di bassa pressione, ed orario per le aree anticicloniche, cioè quelle con area
centrale di alta pressione, è causato dall'accelerazione complementare
(centrifugo-composta) di Coriolis, dovuta al fatto che il sistema di riferimento
terrestre è dotato di moto rotatorio attorno all'asse terrestre. Nell'emisfero
australe, invece, la circolazione dei venti avviene in senso orario per le aree
cicloniche ed antiorario per quelle anticicloniche.
E' importante tenere
presente che un campo di forza rappresentabile come gradiente di una funzione
scalare V (potenziale, cioè energia potenziale per unità di massa o di carica
elettrica) delle coordinate x,y,z, è conservativo, nel senso che la sua
circuitazione (integrale di linea) lungo un percorso chiuso è sempre nulla,
essendo nulla la variazione del potenziale V partendo da un punto e tornando
allo stesso punto . Sono conservativi i campi gravitazionali [G = - grad
V(x,y,z) ] ed elettrostatici [E = - grad V(x,y,z)], ed inoltre i campi
magnetici generati da magneti permanenti, nelle zone di spazio non occupate dai
magneti, e quelli generati da correnti elettriche, lungo i percorsi non
concatenati con i circuiti elettrici . Questo equivale a dire che, se un campo
di forza è conservativo, il lavoro da esso compiuto dipende soltanto dalle
coordinate degli estremi e non dalla forma del percorso lungo il quale si
calcola l'integrale di linea.
In questo caso, poiché la divergenza di un
campo conservativo F è la divergenza del gradiente del campo , si ha:
(div F = div (-grad V) =
= D2x V +
D2yV + D2z V = D V (Laplaciano di V = somma delle derivate parziali seconde
di V).
3) L'operatore rotore (rotazione) di un vettore V, rot
V, rappresentabile formalmente come prodotto vettoriale (nabla ^
V) , dell'operatore nabla per V, è un operatore il cui significato
fisico può essere compreso intuitivamente pensando ad una turbinetta idraulica,
rotellina dotata di palette e posizionata in un fluido (liquido o gas) in moto,
in modo tale che sia libera di ruotare intorno ad un asse fisso. Se il campo di
velocità v(x,y,z) del fluido è irrotazionale, cioè se la velocità del fluido è
una funzione tale che l'operatore rotazione applicato ad essa dia componenti
nulle in tutto il fluido,la turbinetta non ruota e si dice che il campo di
velocità è irrotazionale. Questo equivale a dire, come si può verificare con una
semplice dimostrazione matematica, che il campo di velocità si può rappresentare
come gradiente di una funzione scalare (potenziale di velocità); pertanto, tutti
i campi conservativi sono a rotazione nulla (irrotazionali), e viceversa.
Se
invece la turbinetta ruota, significa che l'andamento del campo di velocità è
tale da favorire la formazione di vortici, che la fanno ruotare per effetto di
una coppia generata dalle forze di resistenza idrodinamica sulle sue palette.
Pertanto, se rot v(x,y,z) = i(dVz/dy - dVy/dz) + j(dVx/dz -
dVz/dx) + k(dVy/dx - dVx/dy) è diverso da zero in uno o più punti del
fluido o in tutto il fluido, si deduce che il campo di velocità è vorticoso nei
punti considerati, come, per esempio il campo di velocità di un liquido in
prossimità dell'orifizio dello scarico di una vasca.
Un altro notevole
esempio di campo rotazionale è dato dal campo magnetico generato da un circuito
percorso dalla corrente elettrica. La legge di circuitazione di Ampere esprime
le proprietà del campo magnetico uguagliando l'integrale di linea
(circuitazione) del campo magnatico lungo un percorso chiuso concatenato al
circuito (filo, spira o solenoide), all'intensità di corrente che genera il
campo magnetico. E poiché il teorema della rotazione (di Stokes) consente di
calcolare l'integrale di linea del campo H lungo il percorso chiuso
attraverso l'integrale di superficie di rot H attraverso una superficie S
qualsiasi che abbia per contorno il percorso chiuso che si considera, il flusso
del vettore rot H = J (x,y,z) attraverso S fornisce il valore
della circuitazione di H, se J (x,y,z) rappresenta il vettore densità di
corrente di conduzione attraverso S.

L'avvicinamento di un corpo carico ad una bacchetta di rame determina
all'interno del metallo, per effetto del campo elettrico, uno spostamento di
elettroni liberi (di conduzione) che si distribuiscono sulla superficie della
bacchetta nella parte vicina al corpo carico, se questo è carico positivamente,
mentre si localizzano nella parte lontana dal corpo carico, se questo è carico
negativamente.
E' importante notare che lo spostamento di elettroni nella
bacchetta di rame si verifica sempre in modo tale da rendere nullo il campo
elettrico all'interno del metallo, in condizioni di equilibrio elettrostatico.
Infatti, se all'interno della bacchetta di rame esistesse un campo elettrico,
gli elettroni continuerebbero a spostarsi liberamente ed il conduttore non
sarebbe più in equilibrio elettrostatico. Questo fenomeno si può spiegare anche
ricorrendo al teorema di Gauss, che richiede che affinchè sia nullo il flusso
del campo elettrico uscente da una superficie chiusa, è necessario che nello
spazio delimitato dalla superficie non vi siano cariche elettriche. Ecco perché
le cariche, in condizioni di equilibrio elettrostatico, si localizzano soltanto
sulla superficie dei conduttori. La risposta alla prima domanda è pertanto
affermativa, in quanto, finchè il corpo carico è posto vicino ad un'estremità
della bacchetta di rame, spostando sulla superficie di essa una sferetta
metallica dotata di un manico isolante e collegata ad un elettroscopio o ad un
elettrometro, si può rilevare che la divergenza delle foglie d'oro dello
strumento è notevole quando vengono esplorate le estremità della bacchetta,
mentre decresce gradualmente fino ad annullarsi nel punto medio di essa. Ciò
prova l'esistenza di una distribuzione di cariche elettriche , con segni
opposti, con una densità superficiale decrescente verso il punto medio. Per
elettrizzare stabilmente la bacchetta di rame, basta toccarla con un dito per un
istante, in presenza del corpo carico inducente. In tal modo la carica elettrica
indotta avente lo stesso segno di quella del corpo carico, si disperde a terra,
e la bacchetta rimane carica stabilmente con una carica di segno opposto
rispetto a quella posseduta dal corpo inducente.
Un altro metodo di carica
per induzione , consiste nel collegare due conduttori con un filo metallico
dotato di un interruttore. Avvicinando un corpo carico ad uno dei due
conduttori, essi si caricano superficialmente di elettricità in modo tale da
rendere equipotenziale (campo elettrico nullo) lo spazio interno ad essi ed al
filo che li collega. Basta pertanto aprire l'interruttore , prima di allontanare
il corpo inducente, per separare stabilmente le cariche indotte, con segni
opposti, che si sono accumulate in superficie.
Suggerisco i seguenti riferimenti:
1) Per la
biologia:
www.dica33.it/argomenti/bio_tecnologie/nuovavita4.asp
www.lescienze.it
www.celera.com
www.celera.com/celera/press_releases
www.sussidiario.it
;
2) Per le tecnologie concernenti le applicazioni delle scienze fisiche nei
settori chiave della produzione industriale (microelettronica,computer science,
telecomunicazioni,reti di computer, satelliti):
www.librishop.it - sezione
scienze e tecnologia (risorse accademiche,bibliografiche e siti web);
3)Per
la fisica fondamentale (subnucleare) (quark,leptoni,bosoni
vettoriali,cosmologia, astrofisica):
Libro on line di Antonino Cucinotta
"Gianni e Giulia innamorati speciali - Affascinati dai misteri dell'universo ci
aiutano a capire com'è fatto e come funziona il mondo fisico"
Quest'opera di
divulgazione scientifica, scaricabile a pagamento dal sito www.librishop.it,
sezione "Offerte e promozioni", comprende la versione testo del sito
www.peoplephysics.com.
Il principio di funzionamento è lo stesso dei display touchscreen. Al di
sotto della superficie isolante sulla quale si fa scorrere il dito c'è un
reticolo di sottilissimi fili conduttori isolati l'uno dall'altro e disposti
come le ascisse e le ordinate di un piano cartesiano.
Ogni punto d'incrocio
tra due conduttori perpendicolari tra loro è individuato da una coppia di numeri
interi (x,y) che forniscono al software la posizione istantanea del dito che è a
contatto della superficie isolante. E poichè il dito (conduttore) costituisce
assieme ai fili che si incrociano al di sotto di esso, un sistema di conduttori
le cui capacità elettriche (tra filo e filo e tra ciascun filo ed il dito) si
incrementano notevolmente rispetto a quelle esistenti in assenza del dito, si
accumulano sui due fili e sul dito microcariche elettrostatiche indotte con
segni opposti, che vengono rilevate dal microchip di pilotaggio del touchpad
fornendo al software la posizione istantanea dell'incrocio selezionato
dall'utente.
Lo spostamento del dito sul touchpad viene pertanto convertito
istante per istante in una coppia x,y utilizzata dal software per spostare il
cursore sul display LCD, come avviene per il mouse e per la trackball.
Premesso che è norma fondamentale di sicurezza stradale ridurre
opportunamente la velocità, in funzione delle condizioni atmosferiche e dello
stato del fondo stradale, già nel rettilineo che precede una curva,
bisogna considerare quanto segue:
Se l'auto è già in curva ed è sul punto di
perdere stabilità per una qualsiasi ragione (perdita di aderenza dovuta al fondo
stradale viscido , brusca sterzata o rilascio dell'acceleratore) bisogna
distinguere i seguenti casi:
1) Auto a trazione anteriore sovrasterzante
In questo caso , le reazioni normali esercitate dal fondo stradale sulle
ruote posteriori (Np) sono inferiori a quelle esercitate sulle ruote anteriori
(Na) (vedi parte sinistra della figura) e l'avantreno tende ad abbassarsi
rispetto al retrotreno (il muso della vettura si abbassa per la compressione
delle sospensioni), in quanto si verifica un trasferimento di carichi dalla
parte posteriore alla parte anteriore della vettura. Pertanto il retrotreno
tende a spostarsi verso il bordo esterno della curva , il che comporta il
rischio di testacoda.
Per ridare stabilità alla vettura bisogna
controsterzare e pigiare leggermente l'acceleratore. Infatti ,
accelerando dolcemente, tanto quanto basta, si trasferisce una parte del
carico dall'avantreno al retrotreno (il muso della vettura s'innalza per
l'estensione delle sospensioni). Queste manovre aumentano l' aderenza delle
ruote posteriori e quindi la stabilità,consentendo di raddrizzare l'auto.
2)
Auto a trazione posteriore sovrasterzante
In questo caso, essendo motrici le
ruote posteriori, non è possibile accelerare, neanche dolcemente, in quanto
l'incremento di forza propulsiva sulle ruote posteriori farebbe ulteriormente
sbandare il retrotreno verso il bordo esterno della curva peggiorando la
stabilità. Pertanto bisogna soltanto controsterzare per raddrizzare la vettura e
completarne la stabilizzazione sempre usando lo sterzo.
3) Auto
sottosterzante
In questo caso, è l'avantreno che tende a portarsi verso il
bordo esterno della curva. Per aumentare la stabilità occorre rilasciare
l'acceleratore e controsterzare. In tal modo, senza agire sul freno, si sfrutta
il freno motore e si ottiene un trasferimento di carico dal retrotreno
all'avantreno e quindi un aumento di aderenza.
In tutti e tre i casi
considerati non è possibile usare i freni per aumentare la stabilità, poichè,già
in condizioni di aderenza critica,verrebbe richiesta, anche in presenza del
sistema ABS,una forza d'attrito non disponibile per le pessime condizioni
dell'interfaccia tra pneumatici e fondo stradale, con il rischio di determinare
lo slittamento del veicolo e la perdita del controllo.La forza di attrito
(aderenza) complessiva durante la frenata è data dalla somma vettoriale della
forza d'attrito (forza centripeta,perpendicolare alla velocità dell'auto e
diretta verso il centro della curva) richiesta per far muovere l'auto lungo la
curva di raggio R, con accelerazione centripeta V2/R, e della forza
d'attrito,diretta lungo la tangente alla curva, che è necessaria per non far
slittare i pneumatici durante la frenata.Se si tiene presente che questa seconda
forza d'attrito, in fase di frenata, può essere sensibilmente maggiore di
quella, uguale e contraria alla forza propulsiva F, che è necessaria per far
avanzare l'auto prima che siano azionati i freni, si comprende come la
risultante delle forze d'attrito tangenziale e radiale,non passando per il
centro della curva e dando origine ad una variazione di direzione della
velocità,tenda a far sbandare il veicolo, rendendolo incontrollabile qualora
siano particolarmente critiche le condizioni del fondo stradale.


Ringrazio sentitamente tutti i visitatori per le lusinghiere attestazioni di gradimento espresse sui contenuti di questo sito.
Nel 1879 il fisico statunitense Hall scoprì che in un conduttore percorso da
corrente elettrica,in presenza di un campo magnetico avente una componente
perpendicolare alla velocità di deriva delle cariche elettriche che
costituiscono la corrente, si genera una differenza di potenziale (tensione)
dovuta ad un campo elettrico (campo di Hall) perpendicolare all'asse del
conduttore.
Esempio: Se il conduttore, costituito da una lamina di sezione
rettangolare con dimensioni a e b, è percorso da una corrente
continua di intensità I ed è sottoposto ad un campo magnetico di
induzione B perpendicolare al lato a ed alla direzione di moto
degli elettroni di conduzione,si genera una piccola tensione continua dovuta ad
un campo elettrico trasversale rispetto alla corrente ed orientato
parallelamente al lato a.
Infatti, se si indica con v la
velocità di deriva degli elettroni di conduzione che costituiscono la corrente
I,questi,essendo soggetti alla forza F = -evB (forza di
Lorentz),dovuta al campo magnetico B e perpendicolare al piano dei
vettori v e B (e è la carica dell'elettrone),si spostano
parallelamente al lato a accumulandosi lateralmente.
Questo accumulo
di elettroni determina una differenza di potenziale VH (di
Hall), quindi un campo elettrico (di Hall) EH =
VH/a, che tende ad equilibrare la forza di
Lorentz.
Pertanto, se si indica con S = ab la sezione del conduttore e
con N il numero di elettroni di conduzione per unità di volume, si
ottiene:
I = SNev; v =
I/(abNe);
eEH = eVH/a = evB =
e I/(abNe) B;
VH = IB/(Neb).
Sull'effetto
Hall, molto evidente nei semiconduttori (germanio, silicio ...),si basa il
funzionamento di sensori microelettronici di vario tipo (di prossimità , di
velocità angolare), di vasto impiego nei sistemi di automazione.
Un conduttore è in equilibrio elettrostatico (le cariche elettriche da esso
possedute sono in quiete),soltanto se il campo elettrico è nullo in tutti i
punti interni ad esso; infatti, se così non fosse, gli elettroni di conduzione,
liberi di muoversi nella banda di conduzione del metallo sotto l'azione di un
campo elettrico, si sposterebbero dando origine ad una corrente elettrica
all'interno del conduttore.
Pertanto, se un conduttore in equilibrio
elettrostatico possiede una carica elettrica acquisita per contatto con un corpo
carico o per strofinio o per induzione, essa deve necessariamente localizzarsi
soltanto sulla superficie esterna.
Questo fenomeno si può spiegare
rigorosamente applicando il teorema di Gauss, che afferma che il flusso del
campo elettrico E uscente da una qualsiasi superficie chiusa al cui
interno siano presenti delle cariche elettriche,con lo stesso segno o con segni
opposti, è dato dal rapporto tra la loro somma algebrica S+/- Qk e la costante dielettrica del vuoto eo:
F(E) =
S+/- Qk/eo.
Esempio: Se consideriamo il caso
particolarmente semplice di un conduttore sferico massiccio di raggio R, il
flusso del campo elettrico uscente da una qualsiasi sfera concentrica di raggio
r < R è dato, grazie alla simmetria sferica,dal prodotto del campo per l'area
della superficie sferica di raggio r:
4pr2E = S+/-
Qk/eo.
Pertanto il campo
E è nullo soltanto se è nulla la somma algebrica delle cariche interne
alla superficie considerata.
Se la sfera possiede una carica elettrica,
questa deve necessariamente localizzarsi in superficie, entro uno strato di
dimensioni comparabili con quelle di un atomo (10-8cm), in modo tale
da rendere equipotenziale lo spazio occupato dalla sfera. Infatti, poichè il
campo elettrico E = -grad V, è dato dal gradiente del potenziale
elettrostatico V cambiato di segno, dovendo essere nullo il campo, ne deriva il
valore costante del potenziale V in tutti i punti interni al conduttore.
Una
conseguenza importantissima di questo effetto è la possibilità di schermare un
corpo dai campi elettrici ponendolo all'interno di un involucro conduttore
chiuso (schermo elettrostatico), continuo o costituito da una rete metallica a
piccole maglie (gabbia di Faraday). Infatti in tal caso, anche se la superficie
conduttrice viene elettrizzata con qualsiasi metodo, le cariche elettriche da
essa acquisite si distribuiscono sempre sulla superficie esterna dell'involucro,
rendendo equipotenziale lo spazio occupato dall'involucro e quindi nullo il
campo elettrico nei punti interni ad esso.
Un osservatore all'interno della
gabbia non rileva pertanto i campi elettrici esterni.
Quanto male nel mondo è stato prodotto e continua ad essere prodotto dalla
mancanza di umiltà e dall'indisponibilità al dialogo con il prossimo, a tutti i
livelli !
La Storia c'insegna che l'orgoglio, la prepotenza e l'avidità di
potere dei dominatori hanno sempre calpestato i diritti dei più deboli, e che ,
a lungo andare, le catene che hanno conculcato la libertà dei vinti, si sono
sempre dissolte, direi quasi per naturale esaurimento della "carica" di potere,
per confermare che l'unico Signore della Storia è Cristo, che è il Principe
dell'umiltà e dell'amore.
In particolare, chi si professa cattolico
deve sempre essere disponibile a condividere con il prossimo i doni che
lo Spirito Santo gli ha elargito.
Come in una macchina ciascun ingranaggio
contribuisce in ugual misura al suo regolare funzionamento, trasmettendo energia
meccanica, così ogni uomo dovrebbe rappresentare per l'umanità un "ingranaggio"
di trasmissione di forza morale , amore ed energia mentale. Purtroppo in questo
mondo dominato dall'egoismo, che è il peggior nemico dell'uomo, siamo, ahinoi,
ben lontani da questo modello ideale. Anzi sembra che oggi più che mai, in
questa prima decade del terzo millennio, pur essendo altissimi i livelli di
avanzamento raggiunti dalla Scienza e dalle varie tecnologie, si sia invece
toccato il fondo del disordine morale, che a partire dal 1968 si è via via
propagato alle colonne portanti della società: famiglia e scuola.
La
famiglia tradizionale fondata sul matrimonio è andata via via disgregandosi
sotto l'effetto della sistematica, direi quasi scientifica irrisione dei valori
religiosi, di fedeltà reciproca, umiltà, condivisione delle responsabilità,
mutua comprensione, incrementando in modo intollerabile l'entropia (in
termodinamica equivale a disordine) del sistema società.
La scuola ha subito
una degenerazione analoga, soprattutto in Italia. Spinte demagogiche, spacciate
per riforme culturali, hanno intaccato sin dal 1962 la struttura
didattico-educativa con l'attuazione della riforma della scuola media inferiore
(che rese prima non obbligatorio lo studio del latino, per abolirlo qualche anno
dopo) e con l'introduzione, nel 1969, del famigerato esame di maturità a menu
(con due materie, di cui una scelta dal candidato), con lo "splendido" risultato
del decadimento culturale che oggi possiamo constatare in vaste aree del sistema
scolastico italiano. Fu mancanza di umiltà il voler imporre ope legis un
degradamento culturale che è alla base del semianalfabetismo di ritorno rilevato
recentemente. Gli effetti di questa lenta ma inesorabile involuzione culturale,
voluta, li possiamo constatare giorno per giorno osservando che gran parte della
nostra gioventù studentesca subisce passivamente il fascino perverso dei
prodotti tecnologici più avanzati ( mi riferisco in particolare ai
videocellulari), senza possedere gli strumenti culturali per dominarli. L'uso
dei prodotti tecnologici deve essere gestito consapevolmente attraverso
il filtro della cultura, non attraverso le trovate commerciali dei gestori delle
società di telefonia cellulare che sembra facciano a gara tra loro per inventare
"la necessità" di nuovi consumi multimediali fini a se stessi, che nulla hanno
di culturale, anzi sono vere e proprie droghe elettroniche che contribuiscono
all'istupidimento dei giovani non dotati di validi strumenti culturali.
La
mancanza di umiltà di molti cattedratici italiani fa sì che molti giovani e
validi ricercatori, vittime del potere accademico, siano costretti ad emigrare
all'estero per fare carriera scientifica.
Io penso che l'umiltà sia un valore
fondamentale, imprescindibile, soprattutto per chi fa ricerca. I ricercatori
sanno benissimo quanto sia impegnativo formulare un'ipotesi scientifica ed
elaborare nuove teorie, sperando che le verifiche sperimentali insite nel metodo
galileiano possano convalidarle, e pronti in caso di insuccesso a formulare
nuove ipotesi, senza stancarsi mai, sempre lavorando con pazienza ed umiltà ,
per tentare di spiegare i misteri della natura. I ricercatori sono motivati da
una vera e propria vocazione per la Conoscenza, che li spinge ad affrontare
continuamente, con grande umiltà, notevoli sacrifici , ed in casi limite anche
rischi mortali (si pensi alle ricerche sui virus).
La stessa umiltà è
necessaria per chi si impegna nella divulgazione scientifica fatta seriamente,
non banalizzando i contenuti, ma cercando sempre la via più efficace e più
diretta, soprattutto attraverso esempi che possano fornire riscontri immediati,
per riuscire a trasmettere il meraviglioso senso del mistero che pervade l'uomo
davanti ai misteri del Creato. La divulgazione scientifica dovrebbe, a mio
parere, giungere nel contempo alla mente ed al cuore di coloro che, con umiltà,
siano disposti a recepirla, rendendosi partecipi della bellezza e del fascino
che solo la poesia della natura, attraverso la scienza, può offrire.
Un pannello fotovoltaico per la produzione di energia elettrica funziona in
base all'effetto fotovoltaico che si verifica in una giunzione semiconduttrice
PN al silicio illuminata dalla radiazione solare. I fotoni della radiazione
elettromagnetica assorbiti dalle celle solari (pile fotovoltaiche), collegate in
serie per costituire un pannello fotovoltaico, cedono la loro energia al
cristallo semiconduttore generando coppie elettrone-buca (una per ciascun
fotone). Gli elettroni e le buche generati in una giunzione PN migrano sotto
l'azione del campo elettrico esistente all'interfaccia tra il silicio di tipo P
(contenente prevalentemente buche, che equivalgono all'assenza di un elettrone
di valenza e quindi ad una carica elementare positiva) ed il silicio di tipo N
(contenente prevalentemente elettroni) e si accumulano rispettivamente nella
zona N e nella zona P, dando origine ad una differenza di potenziale di circa
0,5 V, che aumenta lievemente (con legge logaritmica) in funzione del flusso
luminoso assorbito dalla cella.
Le batteria solare ottenuta collegando le
celle in serie genera una forza elettromotrice con valori standard (12 V , 24 V
o 48 V) ed alimenta attraverso una scheda elettronica di regolazione una
batteria di accumulatori (al piombo, al Ni Cd o di altro tipo), che funge da
serbatoio di energia elettrica durante le ore di buio o in mancanza di corrente
di rete. Tra la batteria di accumulatori e la rete elettrica è collegato un
inverter, che serve a trasformare la corrente elettrica continua in corrente
alternata monofase a 220 V, 50 Hz o trifase (220V/380 V, 50 Hz). I sistemi
fotovoltaici installati dalle società elettriche sono dotati di uno speciale
contatore che registra sia l'energia prodotta che quella assorbita, consentendo
all'utente di conseguire un risparmio in bolletta corrispondente all'energia
prodotta.
E-mail:"Son rimasto letteralmente a bocca aperta nel vedere un sito siffatto.
E' pleonastico farle gli inesplicabili complimenti e congratulazioni per il
magistrale lavoro di divulgazione da lei espletato nello stendere questo sito.
Comunicherò a tutte le persone interessate a conoscere la fisica l'indirizzo di
questo sito ed inoltre farò in modo che i miei figli reperiscano materiale
culturale ai fini didattico/scolastici da questo stesso sito. Peccato però che
la grafica non sia degna di questi magnifici contenuti... Tuttavia la domanda
che le porgo trova la sua ragion d'essere dal fatto che vedo felicemente la sua
disponibilità nel rispondere a domande sul mondo della fisica; e non solo. Lei
ha il grande pregio (forse un dono di Dio) di rendersi disponibile alle persone,
rispondendo con parole degne di un essere speciale, di una persona il cui grande
valore morale è l'umiltà. Da qui nasce il motivo della domanda da me posta; io
sono un docente di filosofia in un liceo. Mio figlio si trova in difficoltà di
fronte a d un dubbio che lo tormenta da tempo e al quale il suo docente di
fisica non ha dato una risposta comprensibile. Mi auguro che lei ci
riesca..."
Risposta:
In un conduttore di lunghezza l, sezione S e
resistività r, gli elettroni liberi (elettroni
appartenenti alla banda di conduzione) , quando sono accelerati dal campo
elettrico E = V/l prodotto dalla d.d.p. V applicata agli estremi, per la
seconda legge della dinamica acquisiscono un’accelerazione a = F/m
= -eE/m , essendo e = 1,6 . 10-19C la carica ed m la massa
dell’elettrone.
Pertanto, se la tensione V è costante, sono costanti anche il
campo elettrico E e l’accelerazione a, e l’elettrone si muove di
moto uniformemente accelerato fino a quando non subisca un urto contro uno ione
del reticolo cristallino del metallo.
Se si indica con t l’intervallo di tempo durante il quale il moto è
uniformemente accelerato (si consideri che la velocità in un moto uniformemente
accelerato è direttamente proporzionale al tempo), si può calcolare la velocità
di deriva v = a t = eEt/m =
eVt/(lm) che l’elettrone acquista sotto l’azione della
d.d.p. V applicata agli estremi del conduttore. Quindi il legame tra la velocità
di deriva v e la d.d.p. V è lineare. E poiché la densità di corrente J (che si
misura in A/mq ed è definita dal rapporto tra l’ intensità di corrente I e la
sezione S) è legata alla velocità di deriva v dalla relazione J = N e v, dove N
è la concentrazione (numero di elettroni di conduzione per m3 nel
metallo considerato), si ottiene l’espressione maxwelliana della I legge di Ohm
J =sE :
J = I/S = Nev = [Ne2t /m](V/l) = sE, dove s = 1/r =[Ne2t /m]( è la
conduttività del metallo.
Si ottiene quindi la I legge di Ohm: I/S =
V/(lr );
V = I (rl/S) = IR
, dove R = (rl/S) è la resistenza del conduttore (II
legge di Ohm).
Pubblico con piacere,su richiesta,l'e-mail inviatami dal
gentilissimo visitatore di Vibo Valentia, che ringrazio di cuore per i
lusinghieri complimenti e per gli auguri pasquali.
Re:"Sono felice di aver
avuto una risposta che ha diradato le nubi del dubbio di mio figlio, il quale la
ringrazia immensamente per la sua chiarezza espositiva e per la sua prontezza
nel rispondere in tempi relativistici alla domanda da me posta circa il legame
tra la velocità di deriva e la d.d.p. Tuttavia pensavo che lei pubblicasse tutto
quello che le ho scritto in questo campo; la pregherei, quindi, se possibile, di
esporre i miei complimenti. Vorrei che i fruitori del sito "vedano" i commenti.
Grazie! Anche se in ritardo, le faccio tanti auguri di buona pasqua."
Si tratta di un fenomeno di capillarità causato dalle forze elettriche di
adesione tra il materiale poroso (la carta) e le molecole d’acqua.
Se
immergiamo un tubicino di vetro con un diametro di alcuni decimi di millimetro
(capillare) in un recipiente contenente acqua, notiamo che il livello raggiunto
dal liquido nel capillare supera di poco quello del recipiente, e precisamente
che il dislivello tra le superfici libere interna ed esterna al tubicino è
inversamente proporzionale al suo diametro.Ciò è dovuto al fatto che le forze
elettriche attrattive che fanno aderire l’acqua alla parete interna del
capillare, bagnandolo, superano le forze elettriche di coesione tra le molecole
determinate dai legami a idrogeno esistenti tra ciascuno dei due atomi di
idrogeno di una molecola d’acqua e gli atomi di ossigeno delle molecole
contigue.
Si tenga presente che se le forze di coesione tra le molecole di
un liquido, responsabili dei fenomeni di tensione superficiale (fenomeni di
superficie), superano le forze di adesione tra il materiale del tubicino e le
molecole del liquido, la superficie libera di questo si incurva (menisco
convesso) senza bagnare la parete, ed il livello interno del liquido si abbassa
rispetto a quello esterno in modo direttamente proporzionale al coefficiente di
tensione superficiale del liquido ed inversamente proporzionale alla densità del
liquido ed al diametro (depressione del mercurio in un capillare). Se invece,
come nel caso dell’acqua in un capillare, le forze di coesione tra le molecole
del liquido sono meno intense di quelle di adesione tra il materiale del
tubicino e le molecole del liquido, la superficie libera di questo si incurva
(menisco concavo) bagnando la parete, ed il livello interno del liquido si
innalza rispetto a quello esterno , secondo una legge analoga a quella che
descrive la depressione di un liquido che non bagna la parete.
L’imbibizione
della carta porosa si spiega considerando che la sua struttura è costituita da
tanti microcapillari che esercitano sulle molecole d’acqua forze di adesione più
intense di quelle di coesione , spingendo verso l’alto il liquido contro la
forza di gravità, finchè la pressione idrostatica generata dall’assorbimento del
liquido da parte della carta non faccia equilibrio alle forze elettriche che
causano il fenomeno.
Il fisico inglese Paul Dirac nel 1928 dimostrò attraverso la sua famosa
equazione, che consente di includere nella meccanica quantistica (o ondulatoria)
formulata dal fisico austriaco Erwin Schroedinger i principi della teoria
einsteiniana della relatività ristretta, come ad una particella elementare con
spin (1/2) come l’elettrone, dotato di carica elementare negativa, debba essere
necessariamente associata “specularmente”, cioè come una sorta di particella
“immagine” riflessa da un misterioso specchio della natura, un’antiparticella
(particella di antimateria) avente la stessa massa, lo stesso spin e carica
elementare positiva. L’antiparticella dell’elettrone, ipotizzata da Dirac e
scoperta da Anderson nel 1933 studiando mediante palloni sonda la radiazione
cosmica, venne denominata positrone (o positone), cioè elettrone positivo.
L’elettrone ed il positrone sono entrambe particelle stabili, proprio perché
sono dotate di cariche elettriche elementari uguali e contrarie, e mantengono la
loro stabilità finchè non collidono tra loro annichilandosi in due fotoni di
alta energia (quanti di radiazione gamma).
In tal caso, infatti, la
particella e l’antiparticella, fatte di massa e di carica, annullandosi la somma
algebrica delle cariche elettriche che le differenziano l’una dall’altra,
perdono la loro stabilità, e l’energia relativistica E =
2moc2 associata alla somma 2mo delle loro masse
a riposo, si libera sotto forma di energia elettromagnetica .
Viceversa, due
quanti di radiazione gamma possono creare una coppia particella-antiparticella
(elettrone-positrone o protone-antiprotone) purchè la loro energia totale sia
almeno uguale alla somma delle loro masse moltiplicata per c2.
Pertanto la materia (o l’ antimateria) di una particella elementare consta di
massa (da sola instabile) e di carica elettrica. In realtà, oltre alla carica
elettrica, intervengono altre “cariche” che impediscono alla massa di
trasformarsi spontaneamente in energia secondo la famosa equazione E =
mc2: sono le cariche di sapore o “sapori” delle particelle, quali i
sapori leptonici associati alle particelle elementari sensibili alle sole
interazioni elettromagnetiche e subnucleari deboli (elettrone, muone, tauone,
neutrino e rispettive antiparticelle) ed i sapori dei sei quark (up, down,
strange,charm,top e bottom) e dei rispettivi antiquark che formano gli adroni
(barioni e mesoni), particelle sensibili all’interazione subnucleare forte
oltrechè a quella elettrodebole (elettromagnetica + subnucleare debole). La
massa da sola è instabile proprio perché sono le cariche elettriche e di sapore
a conferirle stabilità rendendola materia (o antimateria).
Due semplici esempi pratici ci fanno capire il ruolo svolto dalle forze
d'attrito che si manifestano come forze di reazione alle forze motrici: 1)
Quando camminiamo applichiamo al suolo delle forze motrici tangenziali (di
azione) che hanno verso contrario al nostro moto e sono controbilanciate dalle
forze d'attrito radente (di reazione) che il suolo esercita sulle nostre scarpe
spingendoci in avanti;
2)Un veicolo di qualsiasi tipo può avanzare grazie
alle forze d'attrito radente che il fondo stradale esercita tangenzialmente
sulle ruote, alle quali vengono applicate le forze di azione dovute alla coppia
motrice sviluppata dal motore.Le forze di attrito nei punti di contatto tra il
suolo e le ruote impediscono a queste di slittare (almeno fino ad un dato
limite, tanto maggiore quanto maggiore è il coefficiente di attrito statico),
imprimendo al veicolo la forza propulsiva che ne determina il moto.
Pertanto
le forze d'attrito sono forze di reazione ogni qual volta si oppongano alle
forze di azione che producono il moto di un corpo.
La linearità o non linearità della caratteristica di un bipolo non è in
relazione con la tempo-varianza nè con la tempo-invarianza.
Per esempio,un
resistore regolabile è tempo variante indipendentemente dal fatto che la sua
caratteristica I/V sia lineare o non lineare. D'altra parte, se si considera un
bipolo costituito da 2 o più resistori lineari (ohmici) o non lineari (varistori
o VDR) collegati in parallelo o in serie tra loro,in modo tale che possa essere
variato il valore ohmico del resistore risultante a seconda delle esigenze
circuitali,si ha l'esempio di un bipolo tempo variante,rispettivamente lineare o
non lineare
Nel processo di carica di un condensatore si annulla la divergenza della
somma dei vettori J = (densità di corrente di conduzione nei fili che
collegano le armature del condensatore al generatore) e dD/dt (derivata
dell’induzione dielettrica rispetto al tempo).
Infatti la divergenza del
vettore dD/dt, introdotto da Maxwell ,che lo definì densità di
corrente di spostamento, per il teorema di Gauss div D = r, dove r è la densità cubica di
carica elettrica,è uguale alla derivata della densità di carica r rispetto al tempo:
div (dD/dt) = d (div
D)/dt = dr/dt.
Poiché dr/dt (variazione temporale della densità di carica sulle
armature, per l’equazione di continuità, che esprime il principio di
conservazione della carica elettrica,uguaglia la divergenza della densità di
corrente di conduzione cambiata di segno - div J, ne consegue che -div
J = dr/dt = d(div D)/dt.
Pertanto div
J + d(div D)/dt = div (J + dD/dt ) = 0.
Nel caso
dell’induttore il vettore induzione magnetica B è sempre solenoidale (div
B = 0) poichè non esistono poli magnetici isolati e le linee di forza del
campo magnetico sono sempre chiuse.
La teoria delle stringhe , detta anche teoria delle corde, fu formulata dal
fisico Gabriele Veneziano, nel 1968, con la finalità di spiegare le proprietà di
alcune combinazioni adroniche (soggette all’interazione forte) dei quark. La
teoria inizialmente non ebbe successo presso la comunità scientifica
internazionale, anche a causa del fatto che, sull’onda del successo riscosso
dalla teoria elettrodebole di Salam-Glashow-Weinberg, i lavori dei fisici
teorici negli anni ’70 riguardavano prevalentemente lo sviluppo della
cromodinamica quantistica , teoria avente come oggetto lo studio delle
interazioni forti generate dalle cosiddette “cariche di colore” dei quark e
mediate dallo scambio di gluoni, quanti di energia subnucleare aventi massa
nulla e concepiti in analogia ai fotoni, che sono invece i quanti responsabili
delle interazioni elettromagnetiche tra particelle cariche, nell’ambito della
teoria dell’elettrodinamica quantistica , sviluppata negli anni ’40 da Tomonaga,
Schwinger e Feynman.
La teoria delle stringhe, riconsiderata negli anni ’80 e
correntemente denominata teoria delle superstringhe (o delle supercorde) , in
quanto fa parte delle varie teorie supersimmetriche (teorie del supermondo), è
una teoria formulata in un continuum ad undici dimensioni, di cui quattro
coincidono con le coordinate x,y,z,t dello spazio-tempo relativistico, mentre le
altre sette sono, per così dire, dimensioni aggiuntive, che nelle fasi iniziali
dell’evoluzione dell’universo (10-43 secondi dopo il big bang) si
sarebbero “arrotolate” in circonferenze infinitesime per noi attualmente
invisibili, il che comporta che esse per noi siano delle dimensioni nascoste
dello spazio-tempo universale.
Nell’ambito della teoria delle superstringhe
ogni particella elementare ed ogni quanto dei campi delle forze fondamentali
della natura (gravitone per quelle gravitazionali,fotone e bosoni vettori W+, W-
e Z° per quelle elettromagnetiche e subnucleari deboli, gluone per quelle
subnucleari forti tra i quark) vengono considerati come corde, la cui lunghezza
dipende dalla massa-energia della particella. Per capire questo concetto,
bisogna considerare i fenomeni vibratori di una corda, per esempio la corda di
uno strumento musicale. Infatti, come le onde stazionarie (armoniche) generate
da una corda di lunghezza L con gli estremi fissi , pizzicata in un suo punto
qualsiasi ,hanno frequenza multipla della frequenza fondamentale fo =
Vs /l = Vs/( 2L), dove Vs è la velocità del suono nel
metallo e l è la lunghezza d’onda, analogamente le
varie particelle che costituiscono la materia dell’universo corrispondono ad
altrettanti stati vibratori (stati risonanti) di “supercorde”, che possono
essere lineari o ad anello, con la lunghezza della corda o della circonferenza
dell’anello inversamente proporzionali alla massa-energia delle
particelle.
La teoria delle superstringhe potrebbe rappresentare la teoria
supersimmetrica ideale per unificare la teoria relativistica della gravità
(teoria della relatività generale) con la meccanica quantistica e con le teorie
quantistiche dei campi del modello standard (elettrodinamica quantistica e
cromodinamica quantistica).
Infatti, il fatto che la lunghezza minima di una
supercorda non possa essere minore del cosiddetto ”quanto di lunghezza” lp della
scala di Planck (lp = 10-35 metri), implica, in base al principio
d’indeterminazione di Heisenberg Dp D x = h/(2p), che la quantità di
moto p = mv e quindi l’energia cinetica Ec = p2/(2m) = (1/2)
mv2 di una particella (supercorda) non possano divergere
all’infinito. Questo equivale ad affermare che lo spazio-tempo è quantizzato e
che lo era anche al momento del big bang. Come conseguenza della quantizzazione
dello spazio-tempo, presupposto necessario per l’unificazione della teoria
relativistica della gravitazione e della meccanica quantistica, deriva
l’impossibilità di considerare puntiforme l’universo al momento del big bang ,
con fondamentali implicazioni concernenti la temperatura iniziale e l’evoluzione
del cosmo.
Pertanto la teoria delle stringhe include, quantizzandola, la
teoria della relatività generale.
Consideriamo due generatori reali di tensione collegati in parallelo ed
aventi le f.e.m. E1 ed E2 e la stessa resistenza interna
Ri .
In questo caso i due generatori sono equivalenti ad un
generatore avente la f.e.m. Eeq = (E1 + E2 )/2
e resistenza interna Ri/2. Infatti , per il teorema di Millman si
ha:
Eeq = (E1/ Ri +
E2/Ri )/(1/ Ri + 1/Ri ) =
[(E1 + E2 )/ Ri]/(2/ Ri) =
(E1 + E2 )/2 .
Poiché il risultato ottenuto evidenzia
l’indipendenza della f.e.m. equivalente dal valore della comune resistenza
interna, si deduce, nel caso limite di due generatori ideali di tensione, con
Ri = 0 , che Eeq = (E1 + E2 )/2
.
Lo stesso risultato si può ottenere per altra via, considerando la corrente
circolante nella maglia costituita da due generatori reali di tensione collegati
in parallelo ed aventi le f.e.m. E1 ed E2 ( per es. con
E1 > E2) e la stessa resistenza interna Ri:
I = (E1 - E2 )/(2 Ri).
Pertanto la
f.e.m. Eeq è pari alla tensione ai capi dei due generatori, che si
ottiene sommando la f.e.m. E2 alla caduta di tensione I Ri
ai capi della resistenza interna dello stesso generatore:
Eeq =
(E1 - E2 ) Ri /(2 Ri) +
E2=(E1 Ri - E2 Ri +
2E2 Ri)/(2Ri)= (E1 + E2
)/2 .
Due antenne radio alimentate dallo stesso trasmettitore e distanziate tra
loro si comportano come due sorgenti coerenti di onde elettromagnetiche,che
irradiano cioè onde elettromagnetiche che presentano un ritardo costante
(differenza di fase costante) le une rispetto alle altre.
Per effetto di
questo ritardo, una stazione ricevente molto distante dalle antenne, riceve la
somma vettoriale dei due campi elettromagnetici, che corrisponde ad un campo
elettromagnetico risultante la cui intensità varia periodicamente al variare
della posizione della stazione ricevente rispetto alle antenne
trasmittenti.
Si verifica in questo caso un fenomeno di interferenza tra le
onde elettromagnetiche irradiate dalle due antenne.
L'interferenza produce
valori massimi del campo elettrico (interferenza costruttiva),pari al doppio del
campo dovuto ad una sola antenna in tutti i punti tali che la differenza delle
loro distanze rispetto alle due antenne sia pari ad un numero intero di
lunghezze d'onda,intendendosi per lunghezza d'onda (periodo spaziale) lo spazio
l = c T = c/f percorso
dall'onda durante il periodo T (inverso della
frequenza f) di oscillazione del campo elettrico.
Se invece si considerano
tutti i punti tali che la differenza delle loro distanze dalle antenne sia pari
ad un numero dispari di semilunghezze d'onda, si ha interferenza distruttiva ed
ivi il campo elettromagnetico risultante si annulla.
L'interferenza produce
pertanto una distribuzione di energia elettromagnetica che varia periodicamente
in funzione della distanza.

Questi fenomeni di affievolimento ed intensificazione del campo si verificano
in particolare nella ricezione a grande distanza delle onde corte (onde con
lunghezza compresa tra 10 e 100 metri) riflesse dagli strati ionosferici.
In
tal caso i punti della ionosfera nei quali avviene la riflessione delle onde, si
comportano come tante sorgenti coerenti i cui contributi interferiscono
distruttivamente o costruttivamente al variare della distanza della stazione
ricevente (fenomeni di fading).
L'interferenza delle onde luminose si ottiene
con dispositivi ottici particolari,in quanto le sorgenti luminose ordinarie
generano tante onde luminose elementari incoerenti tra loro,che sono emesse
senza coordinamento temporale dai singoli atomi.
Per esempio, si possono
ottenere fenomeni di interferenza su una superficie piana con luce monocromatica
riflessa da due specchi opportunamente inclinati tra loro.
Si osserva in tal
caso un sistema di massimi e minimi di intensità luminosa (frange di
interferenza).

Oggi il metodo più usato per ottenere facilmente l'interferenza delle onde
luminose utilizza la luce dei LASER (Light Amplification by Stimulated Emission
of Radiation), dispositivi funzionanti in base ai principi dell' elettronica
quantistica, che emettono onde luminose coerenti sia spazialmente che
temporalmente, cioè con differenza di fase costante tra loro.
Quando un'onda elettromagnetica viene diffusa da un ostacolo o si propaga
attraverso un'apertura di dimensioni comparabili con la sua lunghezza
d'onda,subisce il fenomeno della diffrazione, che si spiega con il principio di
Huygens-Fresnel, in base al quale tutti i punti dell'apertura o dell'ostacolo
che si trova sulla linea di propagazione dell'onda, diventano a loro volta
sorgenti di onde sferiche elementari, che diffondono l'energia dell'onda
elettromagnetica in tutte le le direzioni comprese nella semisfera avente nel
suo centro l'ostacolo o la fenditura.
Le onde sferiche elementari
interferiscono tra loro dando origine ad una distribuzione di energia
elettromagnetica che presenta periodicamente dei massimi e dei minimi al variare
dell'angolo formato dalla direzione iniziale di propagazione con la generica
direzione che si considera (con un angolo compreso tra 0° e +/-
90°).

Nel caso della diffrazione di un raggio luminoso monocromatico attraverso una
piccolissima apertura, circolare o rettangolare, di dimensioni comparabili con
la lunghezza d'onda e praticata in uno schermo opaco, si può osservare su uno
schermo scuro un sistema di frange di diffrazione, rispettivamente circolari o
rettangolari, che corrispondono a massimi e minimi dell'intensità
luminosa.
Dalla misura della distanza tra la frangia centrale ed una delle
frange successive si può ricavare, in base alla distanza tra l'immagine di
diffrazione ed il piano della fenditura, la lunghezza d'onda della radiazione
luminosa.
Se si opera invece con luce bianca, si osservano sistemi di frange
iridescenti dovute ai diversi massimi di luce prodotti dalle radiazioni di
diversa lunghezza d'onda.

I fenomeni di diffrazione che si ottengono inviando su un cristallo un
sottile fascio di raggi X, che sono onde elettromagnetiche con lunghezza d'onda
compresa tra alcuni centesimi e qualche decimo di nanometro, producono su una
lastra fotografica frange di diffrazione che consentono di ricavare informazioni
sulla struttura dei cristalli e delle molecole (diffrattometria a raggi
X).
Infatti i raggi X che vengono diffusi in tutte le direzioni dai singoli
atomi di un cristallo o di una molecola, interferiscono costruttivamente
soltanto in determinate posizioni angolari rispetto al fascio
incidente,consentendo di ricostruire la simmetria che caratterizza la
disposizione degli atomi.
L’interferenza di due o più sorgenti di onde
elettromagnetiche (onde radio, onde luminose o raggi X) è un fenomeno di somma
vettoriale di campi elettromagnetici (onde elettriche + onde magnetiche con
piani di oscillazione perpendicolari tra loro) che producono massimi e minimi di
intensità della radiazione (frange), connessi a differenze di cammino che sono
uguali, rispettivamente, a multipli pari o dispari della semilunghezza d’onda,
al variare delle coordinate spaziali. Le differenze di cammino tra onde piane
interferenti producono ritardi differenti e quindi differenze di fase che
variano in funzione delle coordinate spaziali.
La diffrazione di un’onda
elettromagnetica è dovuta invece al fatto che il fronte di un’onda piana
propagantesi attraverso un’apertura di dimensioni comparabili con la lunghezza
d’onda, si sparpaglia in tantissimi fronti d’onda sferici elementari che
spiegano la propagazione ondosa in tutte le direzioni al di là dell’apertura ,
nel campo angolare di 180°. Se si considera una qualsiasi di queste direzioni ,
per ottenere la relativa intensità della radiazione è necessario comporre
vettorialmente i singoli campi elettromagnetici elementari dovuti alle singole
onde sferiche che si propagano al di là dell’apertura, con il risultato che
l’intensità varia, con periodicità spaziale, al variare dell’angolo da 0° a +/-
90°, producendo, nel caso di una singola apertura, un sistema di frange di
diffrazione, con un massimo centrale e massimi laterali di intensità
decrescente, che sono tanto più fitti quanto minore è il rapporto tra la
lunghezza d’onda e la larghezza dell’apertura; il che spiega la necessità di
impiegare negli strumenti ottici (telescopi, binocoli, ecc..) lenti e specchi di
apertura tanto maggiore quanto più elevata sia la risoluzione richiesta, proprio
per minimizzare gli effetti della diffrazione e potere osservare i minimi
particolari di un’immagine. Se poi si considera un reticolo di diffrazione,
costituito da tante aperture sottilissime con passo comparabile con la lunghezza
d’onda, è ovvio che per ottenere l’intensità della radiazione al variare della
direzione considerata al di là del reticolo (da 0° a 180°), sia necessario
comporre vettorialmente i campi elettromagnetici dovuti alle onde sferiche
elementari generate dalle singole aperture. Applicando le leggi
dell’interferometria, se la direzione considerata è tale che le differenze di
cammino tra le onde piane prodotte nella stessa direzione dalle onde sferiche
generate per diffrazione dalle singole fenditure, siano uguali a multipli pari
della semilunghezza d’onda, si ottiene un massimo di intensità della radiazione
(interferenza costruttiva), altrimenti si ottengono valori di intensità
decrescenti fino a zero (minimi corrispondenti all’interferenza distruttiva per
direzioni tali che le differenze di cammino siano uguali a multipli dispari
della semilunghezza d’onda).
La modellizzazione della fibrillazione cardiaca si basa sull’applicazione
dell’equazione complessa di Ginzburg-Landau, originariamente introdotta ,
nell’ambito della teoria BCS (Bardeen Cooper Schrieffer) della
superconduttività, per spiegare la transizione di un metallo dallo stato
superconduttivo (annullamento della resistenza elettrica) a quello normale , con
resistenza elettrica diversa da zero.
Questa equazione alle derivate parziali
può essere applicata, in contesti diversi da quello della superconduttività,
allo studio di particolari mezzi continui, come appunto il tessuto cardiaco, che
sono caratterizzati da fenomeni di diffusione di ioni (sodio, calcio, potassio)
attraverso le membrane cellulari,in relazione col cosiddetto potenziale di
membrana,generato dalla differenza delle concentrazioni ioniche interne ed
esterne alle cellule del miocardio.
Si tratta di fenomeni che possono dare
origine a moti a spirale (denominati anche “spiral waves”, termine che
letteralmente significa “onde a spirale”).
Questi moti a spirale sono
descritti dalle soluzioni dell’equazione complessa di Ginzburg-Landau,
considerata sia in assenza di perturbazioni, cioè soltanto sulla base delle
proprietà di autooscillazione del mezzo nel quale avviene la diffusione ionica,
sia in presenza di piccole perturbazioni, costituite per esempio da segnali
elettrici periodici di piccola ampiezza applicati al tessuto. In quest’ultimo
caso, le soluzioni dell’ equazione di G.-L. sono rappresentate da una spirale il
cui centro si sposta con una velocità di deriva (drift) che è massima quando il
periodo dei segnali elettrici applicati è uguale o molto vicino al periodo di
rotazione della spirale. E’ questo il motivo per cui si parla di “resonant
drift” , cioè di “moto di deriva risonante”, relativo alla condizione di
risonanza. I moti ionici a spirale sembrerebbero essere la causa determinante
della fibrillazione cardiaca.
Si pensa inoltre di potere applicare la teoria
della risonanza (o della perturbazione singolare, con una determinata frequenza
di risonanza) alla realizzazione di defribillatori a bassa tensione, capaci di
interrompere le aritmie cardiache semplicemente applicando tensioni periodiche
di piccola ampiezza con frequenza uguale, o quasi, a quella di rotazione delle
spirali ioniche.
Bibliografia:
1)Biktashev V.N. ,Holden, A.V.: “Design
principle of a low voltage cardiac defibrillator based on feed-back resonant
drift” Journal of Theoretical Biology 169 (1994) : 101-113.
2) Holden ,
A.V.:”Defibrillation in models of cardiac muscle”, Journal of Theoretical
Medicine 1 (1997) :91-102.
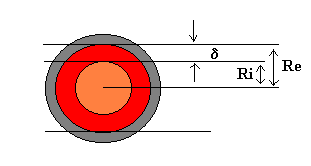
L’ "effetto pelle" (skin effect) consiste nel fatto che la corrente alternata
ad alta frequenza attraversa un conduttore soltanto superficialmente, fino ad
una profondità di penetrazione (delta), che decresce al crescere della
frequenza, a causa del fatto che, quanto maggiore è la frequenza, e quindi
quanto più rapide sono le variazioni temporali del flusso d'induzione magnetica
generato dal passaggio della corrente, tanto maggiore è la reattanza che si
oppone, per la legge di Faraday-Neumann-Lenz, al passaggio di corrente nelle
zone vicine all'asse del conduttore.
La legge che consente di calcolare la
profondità di penetrazione (in cm) d di una corrente
con frequenza f (in Hz) in un conduttore di raggio r e resistività r è la seguente: d = 5033 sqr[r/(mf)], dove m è la permeabilità magnetica del conduttore .
Per il rame
, a 20 °C, d = 6,62/sqr(f) , in cm.
E’ questo il
motivo per cui tutti gli avvolgimenti (bobine) dei circuiti funzionanti a
radiofrequenza ( con f maggiore di 50 MHz) devono essere argentati, proprio per
abbassare la resistenza dello strato superficiale del conduttore e quindi le
perdite per Effetto Joule.
L’esperienza dei fili di Lecher, che si effettua impiegando segnali con
frequenze di qualche centinaio di MHz, evidenzia che con frequenze di tali
valori non è più possibile, come si fa con frequenze più basse, studiare la
linea con la teoria dei circuiti, in quanto il tempo che un’onda
elettromagnetica impiega a percorrere il circuito alla velocità c = 300000 km/s,
non è trascurabile, ma comparabile con il periodo T dell’onda. Per esempio, se f
= 300 MHz, la lunghezza d’onda l = c/f è pari a 1 m. In
tali condizioni il termine radiativo (responsabile della propagazione dell’onda
elettromagnetica) dE/dt (derivata temporale del campo elettrico), che
nella seconda equazione di Maxwell (della circuitazione magnetica) rappresenta
la cosiddetta “densità di corrente di spostamento” (così la denominò Maxwell) ,
non è più trascurabile nel metallo rispetto a quello (J) che rappresenta
l’ordinaria densità di corrente di conduzione, come invece accade per le basse
frequenze . In altri termini si può dire che, se L è la lunghezza del circuito,
il modello a parametri concentrati della teoria dei circuiti è applicabile
finchè il tempo che impiega un segnale elettrico a percorrere la distanza L alla
velocità c, è molto piccolo rispetto a quello impiegato per propagarsi in una
zona di spazio di dimensioni comparabili con la minima lunghezza d’onda.
Se f
= 100 MHz, l = 3 m. Pertanto, essendo in questo caso il
periodo T = 1/f = 10-8 s, per poter applicare il modello a parametri
concentrati le dimensioni del circuito non dovrebbero superare un decimo della
lunghezza d’onda, cioè L = 30 cm = 0,3 m. Infatti in tal caso il tempo impiegato
dal segnale a percorrere il circuito è t=L/c= 10-9 s , cioè un decimo
del periodo, il che equivale a dire che le dimensioni del circuito sono così
piccole che in un istante qualsiasi il campo elettromagnetico propagantesi in
esso si può considerare, in prima approssimazione, di ampiezza costante in tutto
il circuito. Questa condizione non è evidentemente soddisfatta nell’esperienza
di Lecher, che richiede lunghezze maggiori o uguali alla lunghezza d’onda per
potere localizzare nodi e ventri dell’onda stazionaria, per cui il circuito deve
essere schematizzato con il modello a parametri distribuiti (guida d’onda
elettromagnetica).
Un'onda elettromagnetica è costituita da un campo elettrico e da un campo
magnetico che oscillano in piani perpendicolari tra loro,propagandosi nel
vuoto,nell'aria o in qualsiasi mezzo conduttore o isolante e trasportando a
distanza energia elettromagnetica. Il vettore di Poynting rappresenta
matematicamente la propagazione di energia elettromagnetica.
Infatti
l'intensità di un'onda elettromagnetica corrisponde al moduloS del vettore di Poynting ( S = k
EH), che è direttamente proporzionale alle intensità dei campi E e H ,ed è sempre
perpendicolare ad entrambi. Tale vettore fornisce la direzione ed il verso di
propagazione dell'energia elettromagnetica.
Un esperimento semplicissimo per la verifica del principio di Pascal si può
effettuare praticando parecchi forellini in una sfera cava di materiale plastico
del diametro di alcuni centimetri e saldando alla stessa in corrispendenza di un
foro di diametro adeguato una siringa monouso (di materiale plastico). Per
ottenere una saldatura a tenuta d'acqua si può impiegare qualche goccia di colla
acrilica (tipo attak).
Per verificare che una pressione esercitata in un
punto qualsiasi di un liquido si trasmette con la stessa intensità in tutte le
direzioni, basta immergere la sfera in acqua, con lo stantuffo della siringa
tutto abbassato, e riempire di liquido la sfera sollevando lo stantuffo. Si può
verificare che abbassando lo stantuffo,l'acqua zampilla con la stessa intensità
da tutti i forellini, provando così che la pressione esercitata si trasmette
inalterata in tutte le direzioni ( I forellini, almeno una decina, devono essere
praticati uniformemente in tutta la sfera cava).
Il fenomeno dipende dal fatto che le molecole dei gas che costituiscono
l'atmosfera diffondono la radiazione solare in tutte le direzioni con
un'intensità inversamente proporzionale alla quarta potenza della lunghezza
d'onda (diffusione scoperta dal fisico inglese Lord Rayleigh).
E poichè la
luce blu ha una lunghezza d'onda minore di quella della luce rossa, quanto più
spesso è lo strato d'aria attraverso cui si propagano i raggi del Sole, tanto
maggiore è l'assorbimento subito dalla componente blu dello spettro della
radiazione solare.
Ebbene, poichè di giorno i raggi del Sole sono meno
inclinati che al tramonto, essi attraversano uno strato d'aria di spessore
minore che al tramonto; di conseguenza l'assorbimento per diffusione della
componente blu è minore che al tramonto, ed il Sole ci appare giallo (bianco -
blu = rosso + verde = giallo), mentre il fatto che esso scaldi di più dipende
dalla piccola inclinazione dei raggi rispetto alla verticale (cioè allo Zenith
del luogo). Al tramonto invece i raggi del Sole, essendo molto più inclinati che
in pieno giorno, non solo scaldano di meno perchè la loro energia si
distribuisce su una superficie maggiore, ma subiscono un maggiore assorbimento
della componente blu per diffusione, poichè attraversano uno strato d'aria di
spessore via via crescente ; pertanto, con il progredire del tramonto, è la
componente rossa a prevalere sempre di più sulla componente verde residua (che
ha una lunghezza d'onda minore di quella della luce rossa), ed il Sole appare
sempre più rosso.
Il forno a microonde sfrutta l'azione di un campo elettromagnetico ad
altissima frequenza (migliaia di MHz) sulle molecole d'acqua contenute nei cibi
da cuocere o da riscaldare.
Le microonde,che sono le stesse onde
elettromagnetiche sulle quali si basa il funzionamento del RADAR, sono
caratterizzate da una lunghezza d'onda molto piccola, per es. 10 cm se la
frequenza è di 3 GHz = 3000 MHz.
Sono costituite, come qualsiasi altra onda
elettromagnetica (onde radio, raggi X e raggi gamma),da un campo elettrico e da
un campo magnetico che oscillano in piani perpendicolari tra loro propagandosi a
distanza e trasportando energia elettromagnetica.
In un forno a microonde la
radiazione elettromagnetica ad altissima frequenza generata da uno speciale tubo
elettronico, il magnetron (lo stesso tubo impiegato nelle apparecchiature
RADAR), si propaga nella cavità risonante costituita dalle pareti metalliche del
forno,rimbalzando avanti e indietro per effetto delle riflessioni sulle pareti e
generando delle onde stazionarie con nodi (minimi di campo) e ventri (massimi di
campo).
Queste onde elettromagnetiche stazionarie, analoghe alle onde
stazionarie sonore che si generano per riflessione in una canna d'organo o
pizzicando una corda di uno strumento musicale,costituiscono un campo
elettromagnetico i cui punti di massima e di minima intensità sono fissi
all'interno della cavità.
Questo campo esercita forze elettriche sui dipoli
(coppie di cariche elettriche di segno opposto)delle molecole d'acqua, le cui
cariche positive si trovano in corrispondenza degli atomi di idrogeno, mentre le
cariche negative si trovano in corrispondenza degli atomi di ossigeno.
Queste
forze elettriche si comportano analogamente alle forze che il campo magnetico
terrestre (o un qualsiasi altro campo magnetico) esercita sull'ago di una
bussola ,facendolo ruotare.
Pertanto le molecole d'acqua per effetto del
campo a microonde, che ha proprio la frequenza giusta per entrare in risonanza
con i moti rotatori delle molecole, acquistano energia cinetica di rotazione che
si dissipa sotto forma di calore, per effetto dell'attrito con le altre molecole
d'acqua. E' questa l'origine del calore che scalda i cibi fino a cuocerli,agendo
al loro interno e non propagandosi per conduzione, come avviene in un forno
normale, dalla superficie del prodotto sottoposto a cottura verso l'interno.